サンプルサイズ設計基本

  • サンプルサイズ: 研究で収集するデータの件数や参加者数。
  • 小さすぎず大きすぎない、適切なサンプルサイズが必要。
    • 小さすぎる場合
      • 検出力が低くなる（後述）
    • 大きすぎる場合
      • ごく小さな差でも「有意」になり、実質的に意味のない差まで検出
      • 不必要に多くの参加者に介入を行うことは倫理的に問題
  • どうやってサンプルサイズを決める？
    →検定力分析によるサンプルサイズ設計
  • 検定は間違えることがある
  • 検査の間違え方には2種類ある
    • パターン①: 偽陽性（本当はないのに、「ある」と出てしまう）
      • コロナにかかっているか検査をしたら、本当はかかっていないのに検査では陽性になった
    • パターン②: 偽陰性（本当はあるのに、「ない」と出てしまう）
      • コロナにかかっているか検査をしたら、本当はかかっているのに検査では陰性になった
  • 同様に統計的検定も2種類の間違え方をする
    • タイプⅠエラー（αエラー）: 本当は差や効果がないのに「有意」と出てしまう
      • 本当は実験群と統制群の得点に差がないのに、統計的に有意になってしまった
      • 起こる問題: 間違った結論の論文を書いてしまう
    • タイプⅡエラー（βエラー）: 本当は差や効果があるのに「非有意」と出てしまう
      • 本当は実験群と統制群の得点に差があるのに、検定の結果は有意でなかった
      • 起こる問題: 本当は言えたはずなのに、何も結論が言えない
  • αエラーを起こす確率 = 有意水準と同じ
    • 統計的検定では、「もし差や効果がないと仮定したら今回のデータはものすごく低い確率（有意水準: 典型的には5%) でしか出ないようなものだった→差や効果がないと考えるほうが間違っていそう→有意と判断する
    • ということは、差や効果が本当になかったとしても有意になる確率が5%はある
    • ゆえにαエラーを起こす確率 = 有意水準と同じになる
      • 心理学分野では、間違える可能性5%なら許容できるということで、有意水準を5%にすることが多い
  • βエラーを起こさない確率(1-β)を「検出力」という
    • 検出力が足りないと、βエラーを起こしやすくなる
    • 十分な検出力が必要
  • 検出力とサンプルサイズの関係
  • ほしい効果量・事前に決めた有意水準・ほしい検出力の情報があれば、それらを満たすにはいくつデータを取ればいいか（サンプルサイズが）わかる！！！
  • 効果量: 差や効果の大きさを表す指標
    • ひとくちに「効果量」といってもさまざまな種類がある。
      • 分析の目的とデータの種類に応じて使い分けがある。
    • 例: 2群の平均値差に関する効果量でよく使われるのは、Cohen’s d という指標
    • 例: 2変数間の関連の強さの効果量としてよく使われるのは、相関係数r
      • Cohen’s d について授業で使っているスライド

G*Powerによるサンプルサイズ設計

G*Powerとは (Kang, 2021)

  • 検出力分析によるサンプルサイズ設計のためのフリーソフト。GUIのソフトで操作が簡単
  • こちらのページからインストールできる。
  • サンプルサイズ設計には統計学に関する幅広い知識やプログラミング知識が必要だった。
  • ソフトウェアも高額だった。
  • 以下の5ステップでサンプルサイズ設計ができる
  1. 研究の目的と仮説の設定
  2. 適切な検定の選択
  3. 検定力分析の5つの方法の中から1つを選ぶ
  4. 分析に必要な変数を入力
  5. 「計算（calculate）」ボタンをクリック

1. 研究の目的と仮説の設定

  • サンプルサイズ設計の第一歩: 「なにを検討したいのか（研究目的）」と「どのような効果を検出したいのか（仮説）」を明確にすること
    • 例: 本研究では、ある介入（例：利他性を促進するメッセージ提示）が、人々の寄付行動に与える影響を検討することを目的とする。
    • 例: 仮説として、介入を受けた実験群の平均寄付額が、介入を受けていない統制群よりも有意に高いと予測
  • 仮説が明確でなければ、サンプルサイズの検討は意味をなさない
  • 仮説には「片側検定」か「両側検定」かも含める必要がある
  • どのような結果が得られたら仮説が支持されたといえるのかを考え、それに合わせてサンプルサイズ設計をする
    • 例: 実験群の平均寄付額が統制群よりも有意に高いこと（5%水準の両側検定で有意）をもって、仮説が支持されたと判断する

2. 適切な検定の選択

  • 研究目的に応じて、使用する統計的検定の手法を決める。
    • 平均値の比較→t検定（対応あり/なし）
    • 比率の比較→カイ二乗検定やz検定
    • 相関の検定→無相関検定
      • 例: 実験群の平均寄付額と統制群の平均寄付額の比較なので、対応のないt検定

3. 検定力分析の5つの方法の中から1つを選ぶ

  • G*Powerで可能な5種類の分析のうち1つを選ぶ
    • A priori（事前分析）：必要なサンプルサイズを計算（最も一般的）
    • Compromise：検定力と有意水準の両方に妥協してサンプルサイズを決める 
    • Criterion：閾値（例：検定力0.8）を満たす効果量を計算
    • Post hoc（事後分析）：得られたサンプルサイズで検出できる検定力を計算
    • Sensitivity：効果量の検出可能な下限値を推定
      • A priori（事前分析）をして何人分のデータをとればよいか計算

4. 分析に必要な変数を入力

  • 効果量（Cohen’s dなど）、有意水準（α）、検定力（1-β）、標本の割り付け比などを画面にしたがって入力
    • 例: 先行研究と同じくらいの中くらいの効果量、有意水準は一般的な0.05(5%)検出力も一般的な0.8(80%)

5. 「計算（calculate）」ボタンをクリック

  • 必要な情報を入力してボタンを押すと、すぐに結果が出る。

複雑なサンプルサイズ設計

交互作用効果 (Sommet et al., 2023)

交互作用効果を検出するための検定力分析に特化して、適切なサンプルサイズ設計の方法とよくある間違いを解説した論文。

  • 心理学や社会科学では、交互作用効果を検討することがよくある。
  • それにも関わらず、交互作用効果を検出するための適切な検定力分析がほとんど行われていない。
  • 交互作用効果は主効果よりも効果量(f^2)が小さい傾向にあるので、主効果に基づいた検定力分析では人数が不十分なことがある。
  • なにを知りたいかに合わせて検出力分析をすべき。
  • 具体的な提案:
    • 小（small）: f2=0.02 の効果量を設定。
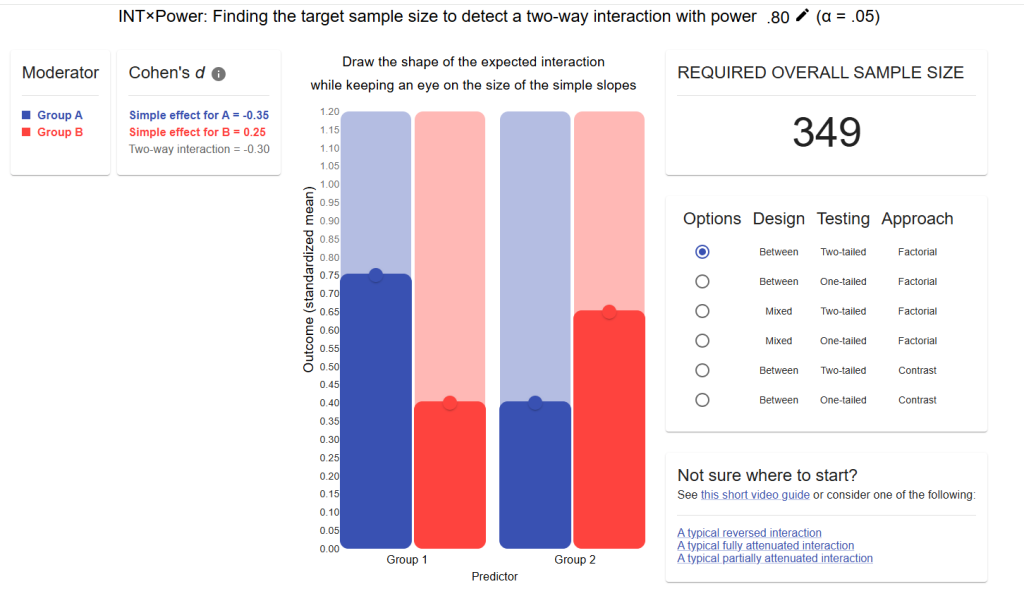
  • 視覚的に使いやすいツールとしてINT×Powerというウェブアプリが紹介されていた（。今後のバージョンでは3要因の交互作用、3水準以上、調整変数、ロジスティック回帰やポアソン回帰にも対応予定らしい。

混合効果モデル

  • 階層構造をもつデータ（級内相関のあるデータ）は必要サンプルサイズが多くなる
    • 各データポイントが独立していないので、情報量がサンプルサイズ分ない
      • 生徒（Level 1） が クラスまたは学校（Level 2） に所属
        → 生徒の成績や態度が教師や学校特性に依存する
      • 個人（Level1) がグループ (Level2) で実験に参加
        →グループ内での相関が高くなる
      • 商品購入データ（Level 1） が 消費者（Level 2） にネスト

→消費者によって買い物の傾向が違う

Summary-statistics-based power analysis (Murayama et al., 2023)

  • 混合効果モデルの検定力分析は難しい。
    • 知識的にも。
    • 既存のツールでは入力しないといけないパラメータが多い（12項目も入力しないといけないツールもある）が、それらは先行研究で報告されていないことが多い。
  • そこで、先行研究のt値とサンプルサイズの情報だけを使って、新しい研究に必要なサンプルサイズを計算する方法を提案。
  • Summary-statistics-based power analysis for mixed-effects modelling

Rパッケージの紹介

simrパッケージ (Green & MacLeod, 2016)

  • GLMM（またはLMM）における検定力分析
    • 固定効果・ランダム効果を組み合わせたモデル（混合モデル）に対応
    • 正規分布ではない応答変数（例：2値、カテゴリデータ）もOK
  • シミュレーションによる検定力分析を行う
    • 効果が存在すると仮定し、応答変数をシミュレーションで生成
    • 生成されたデータに再度モデルを適用
    • 統計的検定を行う

を繰り返し、効果があるときにどれくらい検出できるか（検定力）を求める

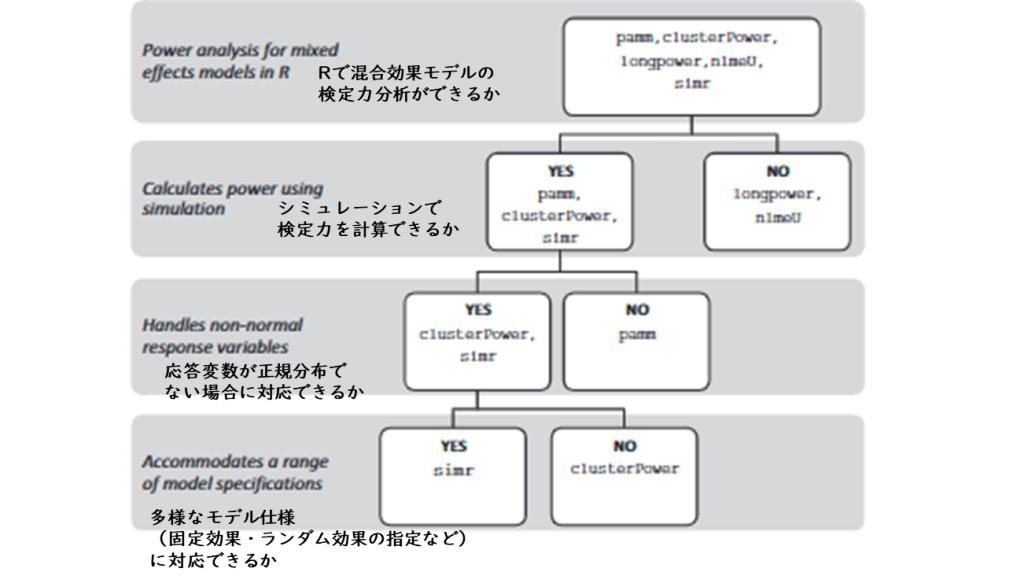
他パッケージとの比較 (Green & MacLeod, 2016)

  • チュートリアルにしたがってやってみた
    • ① パッケージの読み込みとサンプルデータの準備
      • simdataというサンプルデータがパッケージに付属
install.packages("simr")
library(simr)
data(simdata)

> head(simdata)
y x g z

1 8.139081 1 a 3

2 7.947861 2 a 3

3 9.283638 3 a 3

4 7.779489 4 a 2

5 5.803512 5 a 3

6 6.131720 6 a 2
  • ②モデルを適合させる（今回の場合は、切片に群のランダム効果を仮定したポアソン回帰モデル）

model1 <- glmer(z ~ x + (1 | g), data = simdata, family = poisson)

summary(model1)

  • ③効果量を指定する（ためしにx <- -0.05)

fixef(model1)["x"] <- -0.05

  • ④検定力を出す
set.seed(123)  

powerSim(model1)

    33.40% (30.48, 36.42)

Test: z-test

      Effect size for x is -0.050

Based on 1000 simulations, (0 warnings, 0 errors)

alpha = 0.05, nrow = 30

Time elapsed: 0 h 1 m 9 s
  • やってみてわかったこと
    • まずは、モデルを指定する。　
    • 次に、必要な効果量（固定効果の傾きなど）を指定する。
    • 検定力を知りたいとき（この数で足りるか？）は、powerSim(モデル名)
    • 必要な数を知りたいときは、powerCurve(モデル名, along = “ランダム効果があればその単位”, breaks = c(人数の範囲))
      • 人数のシミュレーションにはすごく時間がかかる

mlpwrパッケージ (Zimmer et al., 2023)

  • surrogate modelingを使って少ないシミュレーションで複雑なモデルの検定力分析をする。
  • 任意の統計モデル（lmer, glmer, brms, rstan, lavaan など）を使える。
  • 複数の要素の最適化（予算など）も可能
    • 予算の制約下で、最大の検出力を持つ設計を自動で探す
  • 具体例１: 項目反応理論におけるサンプルサイズ設計
    • find.design 関数で以下のように書くだけで、人数を出力してくれる。計算は230秒。探索範囲を指定する (c(100,500)部分）。
res <- find.design(simfun = simfun_irt, boundaries = c(100, 500), power = 0.95)

summary(res)

Call: find.design(simfun = simfun_irt, boundaries = c(100, 500), power = 0.95)

Design: N = 331

Power: 0.95009, SE: 0.00414

Evaluations: 4000, Time: 229.84, Updates: 16

Surrogate: Logistic regression
  • 具体例2: 国ごとのマルチレベルモデルにおける国と参加者数のサンプルサイズ設計
    • 予算を指定したいときは、以下のように設定する
costfun_multi <- function(n, n.countries) {

  n * n.countries * 5 + n.countries * 1000

}

res <- find.design(

  simfun = simfun_multi,

  costfun = costfun_multi,

  boundaries = list(n = c(20, 300), n.countries = c(4, 30)),

  power = 0.95,

  evaluations = 6000

)
#探索時間は約689秒

Call: find.design(...)

Design: n = 92, n.countries = 14

Power: 0.9491, SE: 0.00598

Cost: 20440

Evaluations: 6000, Time: 689.04, Updates: 32

Surrogate: Gaussian process regression

サンプルサイズ設計と事前登録

結果を見てからサンプルサイズを変えてはいけない

統制群と実験群の差を検定するために、20人を対象に 10回の実験を行う。 有意な場合はそのまま報告するが、有意でなかった場合は サンプルサイズを各条件で一つずつ大きくし、 もう一度検定を行う。有意になるまで検定と実験を繰り返していく。

  • 上記の場合にタイプⅠのエラー確率 (本当は有意でないのに有意だと言ってしまう間違い）がどのように変化するのか、シミュレーションで確認 (小杉・紀ノ定・清水, 2023; pp229-230)
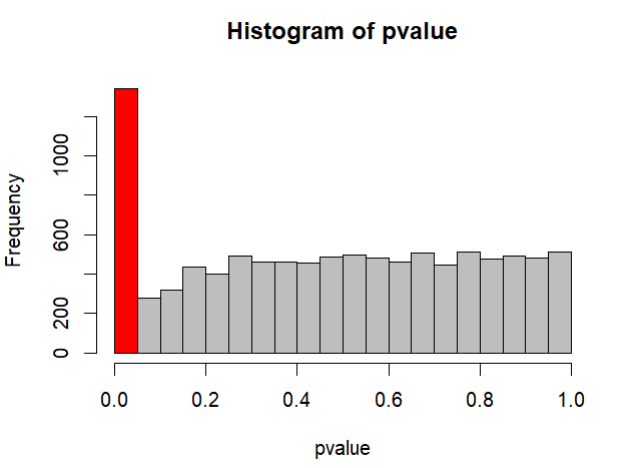
  •  タイプⅠエラーを起こす確率が13.4%まで跳ね上がり（本来であれば5%）、10000回シミュレーションして出てきたp値の分布も値が小さなところに集中していておかしい（本来であればエラー確率が一定: 一様分布になるはず）

事前にサンプルサイズ設計→事前登録

  • 「自分はこれくらいのエラー確率で検定をしますよ」というのを事前登録しておく
  • 事前登録研究はそうでない研究に比べて検定力分析を行っている割合が高く（55% vs 23%)、サンプルサイズが大きかった（平均959.0 vs 536.6) (Van Den Akker et al., 2023)

実際にした登録1

 効果量d

 Chen et al. (2009) で報告されている①t値を元に効果量dを算出したところ1.12であったことから、大きい効果量の目安である0.8とした。 

有意水準α 

0.05に設定した。

検出力(1-β) 

0.8～0.9に設定した。 

級内相関 (ICC)

Chen et al. (2009)ではグループごとの貢献額のICCが報告されていなかったため、水野・清水 (2021b) の本研究のフェーズ2に該当するピリオド6～ピリオド10の級内相関をHAD (清水, 2016) で計算した。算出された②ICCは.76 (95%CI[.60, .87]) であった。ICCが大きくなるほど必要サンプルサイズが大きくなるため、上限である.87に設定した。 サンプルサイズの算出にはR3.6.0 (R Core Team, 2019) および宇佐美 (2011) の式(22)を使用した。検出力が0.8の場合のサンプルサイズは184名 (4名×46グループ)、0.9の場合のサンプルサイズは240名 (4名×60グループ) であった。検出力 (1-β) の上限は0.9とした。 よって本研究のサンプルサイズは、上記の効果量d、有意水準α、級内相関 (ICC) のもとでの③検出力(1-β)の下限が0.8、上限が0.9になるように、少なくとも184名(46グループ)、目標は240名 (60グループ) に設定する。募集人数は230名～300名である。

①t値→d　

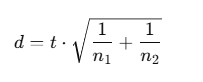
②より必要サンプルサイズが大きくなるように、信頼区間の上限を使った。

③実際に何人のデータがとれるかは幅があるので、検出力の下限と上限を設定してサンプルサイズを決定した。

実際にした登録2

We conducted a pre-test power analysis for Mixed-Model. The effect size was set at 0.20, which is the standard for small effect size, based on Study 1 (effect size was almost 0); the within-class correlation (ρ) was set at 0.43 based on Study 1; the significance level (α) was set at 0.125 because four tests will be conducted; and the power (1-β) was set at 0.8. As a result, the required sample size was estimated to be N=6390. However, due to the limited experimental funding we can only collect N=800 data. With this sample size, we can only detect d=0.568 with 80% probability, but in this study we will post once a recruitment for participation in the experiment with a maximum of 800 people. Since it is not known whether 800 participants will be obtained or how many will drop out of the experiment, we plan to conduct a post power analysis. 

混合モデルに対して事前の検定力分析を実施した。 ①効果量は0.20に設定した。これは、小さい効果の基準値であり、Study 1において効果量がほぼ0であったことに基づいている。クラス内相関（ρ）は、同様にStudy 1の結果に基づき0.43とした。 有意水準（α）は4つの検定を行う予定であるため0.125に設定し、検出力（1-β）は0.8とした。 その結果、②必要なサンプルサイズはN = 6390と推定された。 しかし、実験に使用可能な資金に限りがあるため、収集可能なデータ数は最大でN = 800である。 このサンプルサイズにおいては、効果量d = 0.568であれば80％の確率で効果を検出できる。 本研究では、800名を上限とした参加者募集を一度のみ行う予定である。 なお、800名すべてを確保できるか、あるいは脱落者がどの程度生じるかは不明であるため、事後の検定力分析（post-hoc power analysis）を実施する予定である。

①自分の前の実験を根拠に効果量を設定。

②必要サンプルサイズが非常に多く現実的に無理な数（6390！)だったので、その人数で検出できる効果量を正直に書いた。（今回の実験では、大きな効果量しか検出できない限界点がありますということ）