はじめに
この記事は、Stan Advent Calendar 2019 20日目の記事を修正・加筆し、再アップしたものです。
この記事では、Fehr & Schmidt(1999)の社会選好モデルのパラメータである「妬みパラメータ(自分の利得が相手より少ないのが嫌だと感じる度合い」と「罪悪感パラメータ(自分の利得が相手より多いのを嫌だと感じる度合い」の個人差を、二択課題のデータから階層モデルを用いて推定する方法を紹介します。
Fehr & Schmidt(1999)のモデルは、社会心理学の分野でよく使われる社会的価値志向性(SVO)のモデルのひとつと数学的に等しいことが示されており(武藤, 2006)、推定されたパラメータ値を使った研究の可能性が広がります。
不平等な分配は嫌われる
- 5000円もらう
- 10000円もらう
「1か2のどちらがいいか選んでください」と言われると、よほど奇特な人でない限り2を選ぶはずです。では、次の例ではどうでしょうか。
- あなたもAさんも5000円もらう
- あなたは10000円、Aさんは15000円もらう
今度は、1を選ぶ人も出てきたのではないでしょうか。同じように、
- あなたもAさんも5000円もらう
- あなたは15000円、Aさんは10000円もらう
でも、なんとなく申し訳ない気持ちになって1を選びたくなるはずです。
社会選好と効用関数
なぜこのようなことが起こるのでしょうか。それは、同じ「10000円」であっても、自分のもらえる金額と他者がもらえる金額に差があることによって効用(人がある財を消費したときに得られる満足感のこと)が元の10000円から下がってしまうためです。
このような、他人の利得が自分の効用に影響するような選好のことを社会選好といいます。
そして、どのように自分の利得と他人の利得のバランスを自分の効用として扱うかを表す関数が、社会選好の効用関数です。
代表的なものが、以下のFehr & Schmidt(1999)のモデルです。

この式にある「妬みパラメータ(自分の利得が相手より少ないのが嫌だと感じる度合い」と「罪悪感パラメータ(自分の利得が相手より多いのを嫌だと感じる度合い」の値を個人ごとに推定します。
行動データ
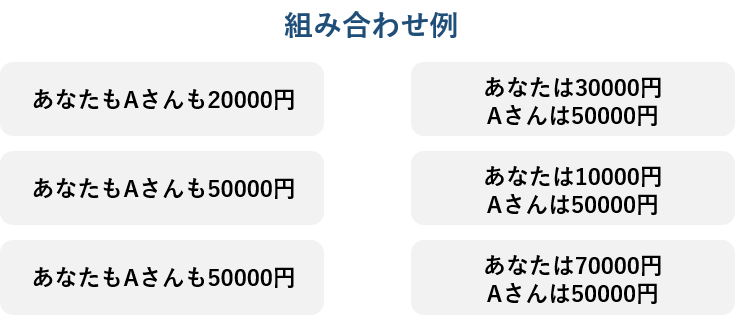
二択課題

このような二択の課題を、金額の組合せを変えて計40回行います。
確率モデル
二択の課題なので、回答者の選択はベルヌーイ分布に従います。

このとき、回答者が不平等分配を選ぶ確率は

と表されます。このU^i_t(不平等分配の効用)に、先程のFehr&Schmidt(1999)のモデル

を入れます。U^e_t(平等分配の効用)については、客観的な金額と等しいと考えます。
RとStanによるパラメータ推定
長くなりましたが、ここからいよいよRとStanを使ってパラメータの推定を行います。
CSVファイルを二つ用意する
実際の二択の行動データが入っているファイル(data.csv)と、金額のセッティングをするファイル(setting.csv)の二つのファイルを用意します。
行動データが入っているファイル(見本)
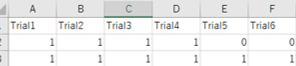
金額のセッティングをするファイル
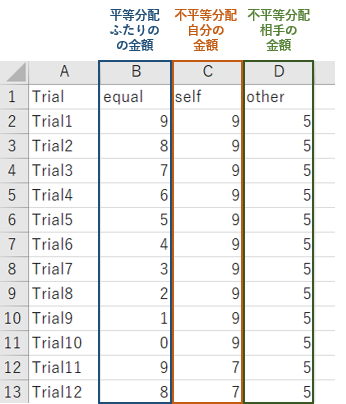
データの読み込み
これら二つのファイルをRで読み込みます。
//data
data <- read.csv("data.csv")
setting <- read.csv("setting.csv")
Stanコード
data{
int Trial;
int N;
real equal[Trial];
real other;
real self[Trial];
int<lower=0,upper=1> choice[N,Trial];
}
parameters{
vector[N] alpha;
vector[N] beta;
vector<lower=0>[N] lambda; //合理性パラメータ
real mu_alpha; //妬みパラメータの平均値
real<lower=0> sigma_alpha; //妬みパラメータの標準偏差
real mu_beta; //罪悪感パラメータの平均値
real<lower=0> sigma_beta; //罪悪感パラメータの標準偏差
real<lower=0> mu_lambda; //合理性パラメータの平均値
real<lower=0> sigma_lambda; //合理性パラメータの標準偏差
}
model {
real u_equal; //平等分配の効用
real u_inequal; //不平等分配の効用
for (t in 1:Trial) {
u_equal = equal[t]; //平等分配の効用は客観的な金額と等しいと仮定
for(n in 1:N){
vector[2] vec_alpha;vector[2] vec_beta;
vec_alpha[1] = other-self[t];
vec_alpha[2] = 0.0;
vec_beta[1] = self[t]-other;
vec_beta[2] = 0.0;
u_inequal = self[t] - alpha[n]*max(vec_alpha) - beta[n]*max(vec_beta);
target += bernoulli_logit_lpmf(choice[n,t] | lambda[n]*(u_inequal-u_equal));
}
}
target += normal_lpdf(alpha | mu_alpha, sigma_alpha);
target += cauchy_lpdf(sigma_alpha | 0,5);
target += normal_lpdf(beta | mu_beta,sigma_beta);
target += cauchy_lpdf(sigma_beta | 0,5);
target += lognormal_lpdf(mu_lambda|0,10^2);
target += cauchy_lpdf(sigma_lambda | 0,5);
}
R側(Stanに渡すデータ)
//datastan N <- nrow(data) equal <- settings$equal other <- setting$other self <- settings$self choice <- data datastan <- list( Trial = 40, N = N, equal = equal, other = other, self = self, choice = choice )
サンプリング
// MCMC sampling
model <- stan_model("model.stan")
fit <-
sampling(
model,
data = datastan,
chains = 4,
cores = 4,
iter = 11000,
warmup = 1000
)
推定結果
上記の手法で個人ごとの妬みパラメータ(α)と罪悪感パラメータ(β)を推定したところ、下図のようになりました。
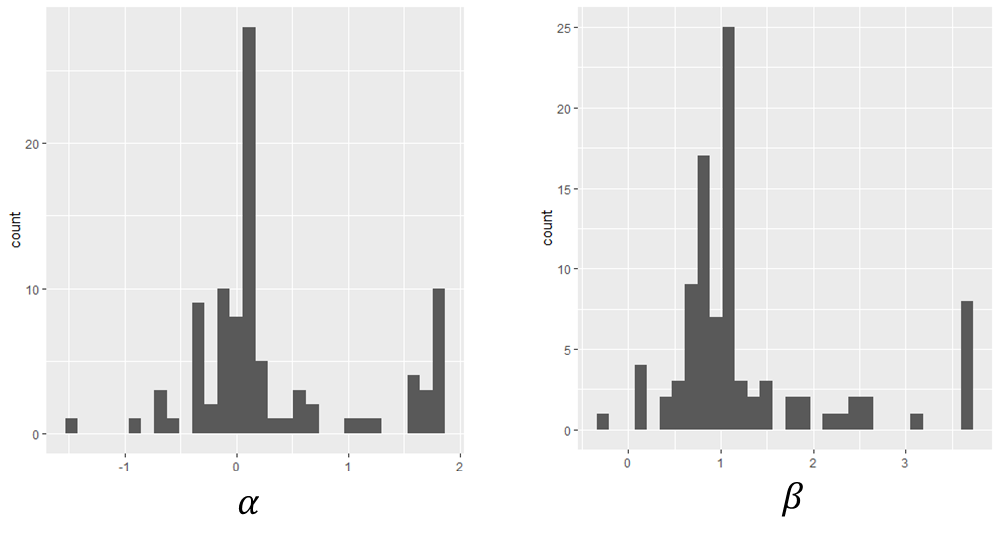
参考文献
Fehr, E., & Schmidt, K. M. (1999). A theory of fairness, competition, and cooperation. The quarterly journal of economics, 114, 817-868.
武藤 正義 (2006). 多様な社会的動機の基礎理論 . 理論と方法 , 21, 63-76.


コメント